History
The construction of the defensive walls in Trzcińsko (Bad Schönfließ in Neumark) probably began at the turn of the 13th and 14th centuries, although the first mention of its existence dates back to 1349, when the construction of the mill at the moat was allowed. Stone fortifications were preceded by timber and earth ramparts, which was most probably created after the foundation of the town in the second half of the 13th century (the first information in documents about the town was recorded in 1281).
In the second half of the fourteenth and the first half of the fifteenth century, the walls underwent minor modifications, perhaps a new crossing at the Strzeszów Gate was pierced, all the gates were raised to the first, open defense levels and the first stage of the Stork Tower was built. The walls were probably significantly damaged in 1433 and 1468. In 1433 it was destroyed by the Hussites, and thirty-five years later by the Pomeranian army. Therefore, from 1483 the fortifications were extended, gradually adapting them to fight with the use of firearms. The gates were raised by the upper polygonal part and the foregates were built with the necks. At the same time, four half towers were transformed into closed towers.
In the early modern period, the walls became less important, but in 1860 the Myślibórz Gate was renovated. In the nineteenth century, gradual liquidation of fortifications began. In 1870, the Strzeszów Gate was pulled down, and at the end of the century, moats and earth ramparts were liquidated. The last significant demolition took place in 1918, when the eastern wall of the Myślibórz Gate’s neck was demolished and in the years 1924-1925. In 2012, a comprehensive renovation of the walls was carried out.
Architecture
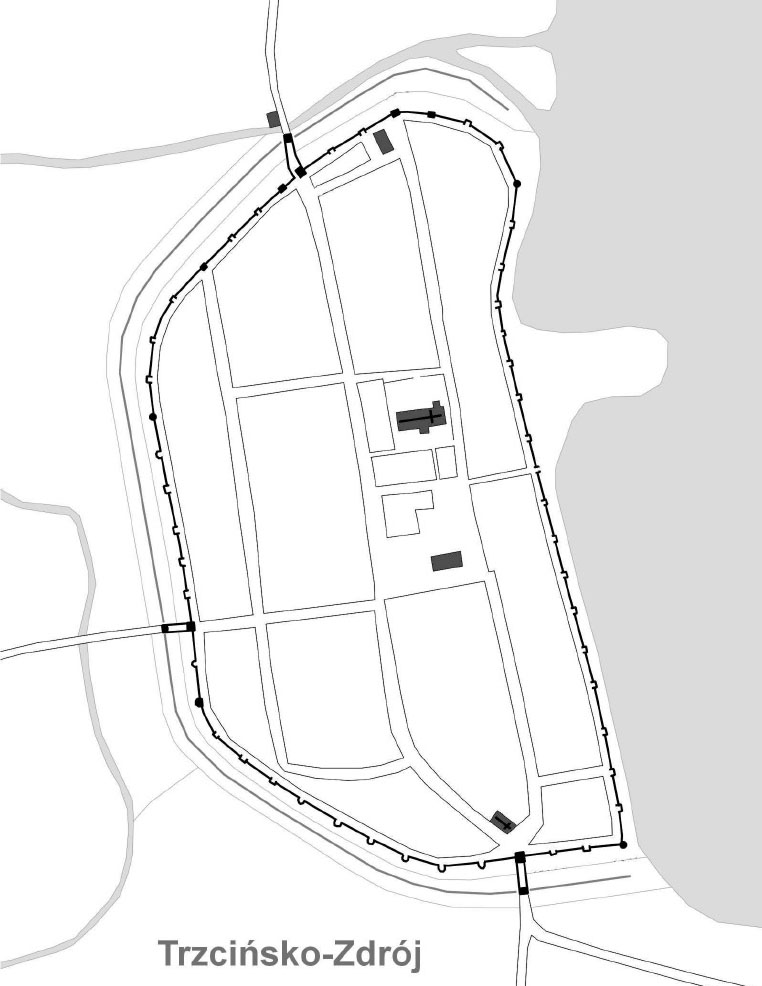
The ring of fortifications was similar to the semi-circle adjacent to the lake. It occupied an area of approximately 18 ha. The main axis of the town, 652 meters long, was set in the north-south direction, the width was 322 meters. From the east, a natural obstacle for the attackers was formed by the lake, while on the other sides the walls were reinforced by a moat. In the vicinity of the town there were also field fortifications, the so-called Landwehr, recorded already in 1318, composed of a earth ramparts and a ditch. The total length of the town walls erected at the turn of the 13th and 14th centuries was 1697 meters.
The walls, with a thickness of 0.9 to 1.2 meters, were built of erratic stones laid in layers, leveled with a thin layer of small pebbles. Inside, the opus emplectum technique was used – the face of the wall was made of stone and the interior was filled with debris bonded with lime mortar. The gates and towers were built partly of stone and partly of gothic brick. Originally, the height of the defensive wall was about 9 meters. It ended straight, without battlement. Along the walls, there was an underwall street to facilitate communication in the event of a siege.
The wall was reinforced by 51 regularly spaced, open half towers, including at least ten semicircular and thirty-nine rectangular. The towers were erected at fairly regular intervals that allowed to defend themselves, but not larger than the double distance from the crossbow. In the fifteenth century, four half towers, among others Stork and Powder, were rebuilt into closed one. With a high degree of probability in the final form, around the mid-sixteenth century, in the fortifications of Trzcińsko there were 43 half towers, including eight semicircular and 35 rectangular, and eight closed towers, including three cylindrical, one semicircular and four rectangular.
A typical rectangular half tower was a rather low projection of the wall, probably two or three-story, without a wall from the side of the town or closed by timber or a half-timbered wall. The first storey served as a handheld weapons warehouse, and the two upper ones were defensive – it had simple slotted shooting holes. Access to the floors was possible from the ground floor, using ladders or brick staircases, or from a hypothetical defensive porch along the wall at the level of the second floor. The whole of the half tower could be covered with a roof. A similar arrangement also had semicircular half tower, except that it forehead was erected on the projection of a circle.
From among the full towers, the Ice Tower (West) represents a derivative type, created from the reconstruction of an earlier object. It is a two-step facility, 14 meters high. The first stage, founded on a semi-circle projection with a width of 4 meters, is two-storey, stone from the outside, with shooting holes and walls up to 1.2 meters thick. From the town side it is brick with two entrances: in the basement and in the second storey. The upper one was the original entrance located at a height of 5 meters. The second stage, completely brick, oval, single-story, was separated from the lower part by a cornice. The whole was topped with a soaring cone of 4.5 meters high with an exit opening to the terrace. Inside, the original ceilings were timber.
The Powder Tower (Pulverturm) was erected at the end of the 15th century, also due to the closing of the semi-circular half window from the beginning of the 14th century. It was erected on a round layout with a diameter of 5.8 meters. It is a three-story building with a height of 16.5 meters. The lower part, which is a remnant of the old half tower, is built of erratic stone. Above the brick section with slot-shaped arrowslits, is topped with a defensive terrace finished with a battlement. The whole was covered with a slender brick cone. There are two entrance openings to the tower: from the ground floor and in the second floor from the old timber platform along the town wall.
The Stork Tower represents a two-step type and is 13 meters high. A two-storey lower stage with a height of 6.5 meters was created on a rectangular plan with dimensions of 5.2 on 5.4 meters. It is made of stone with corners and an inner wall of bricks. Above there is a brick upper stage, also two-storey, ended with a straight wall. From the town side and field side, the tower is closed with straight walls. In the outer façade there are three pairs of slotted arrowslits. From the upper step grows an octagonal pyramid.
The walls were provided with three gates: Myślibórz Gate (also called Stone) from the south, Chojeńska (Rosnowska) from the west and Strzeszów Gate from the north. In one of the half towers from the side of the lake, there was a water wicket gate, also called Bath Gate. In the fifteenth century, the gates were raised with polygonal parts and reinforced with foregates, connected with the appropriate gates by the necks. The construction of foreground observation points was forced by the widespread use of firearms.
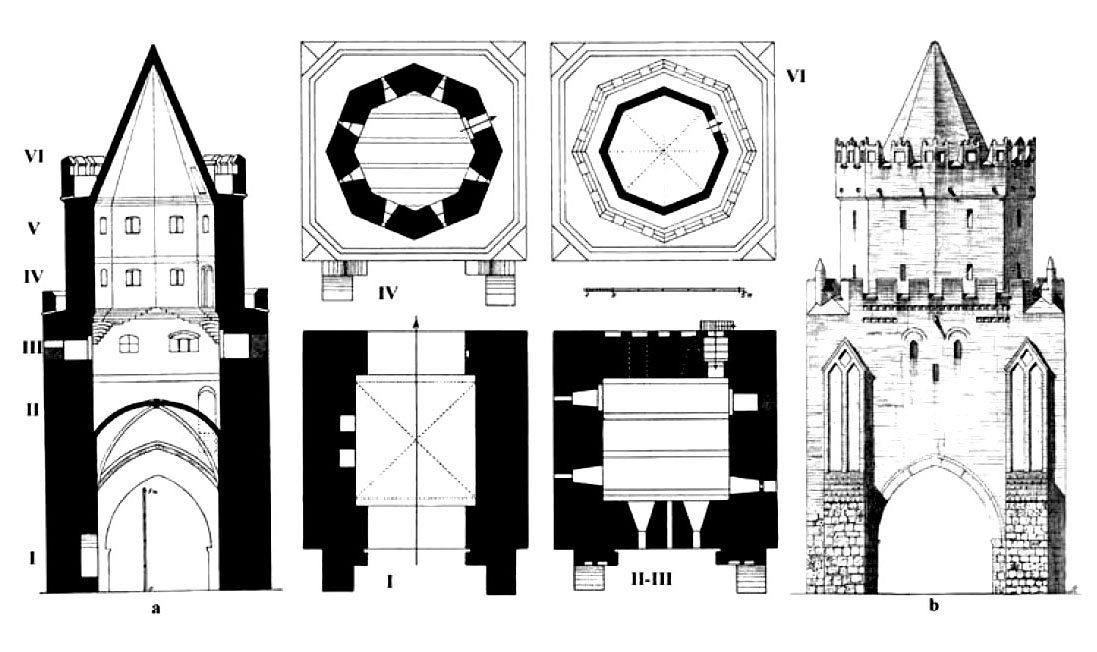
The Myślibórz Gate complex consisted of an internal gatehouse, a gate’s neck and a front gatehouse. The proper gate represents a tower type, two-stage, on a rectangular plan with dimensions of 8.7 to 8.3 meters with a height of 21 meters. The lower stage, in the shape of a cuboid with a height of 11 meters, consists of two parts: the lower part, made of granite, holding the passage and the entrance from the east, and the upper, two-story brick part, ending with an octagonal defensive porch decorated with a brick frieze. The passage has a width of 3.7 meters and a height of 4.4 meters. From the angular part, an eight-sided brick part grows, crowned with battlement and a pyramid. In the outer facade there are two buttresses with guides of the former portcullis, higher decorated with blendes. Three slotted arroowslits were placed just below the defense porch. In the inner façade there are two rows of ogival blendes. On the eastern side, at the level of the second storey, there is a hole that most probably remains of the latrine. Inside the rib vaulted passage, are the remains of an oak door, blocked with stone boulders protruding from the face of the wall. Connections between levels were solved using ladders. There are shooting arrowslits on each side of the upper part of the gatehouse.
The complex of the Chojeńska Gate also consisted of an inner gate, a neck and a outer gategouse. The internal gatehouse represents a tower type, two-stage, on a rectangular plan with dimensions of 7.3 on 6.9 meters, with a total height of 17 meters. The lower, three-storey stage of the gatehouse consists of two parts: the lower one, with a brick passage, 3.2 meters wide and 4 meters high, and the upper brick one. The external façade is without decorations, it has only two brick buttresses, which are remnants of the gates’ neck, with traces of the portcullis guides. The internal façade has an entrance opening in the first floor and a row of four high blendes above. The rectangular part ends with an octagonal, two-story part with a height of 4.8 meters. On its sides there are slotted arrowslits. The top step is crowned with battlement, under which an openwork frieze runs. The entire building is crowned with an octagonal pyramid of 3.6 meters high.
The not existing anymore Strzeszów Gate complex was an inner gatehouse, a neck and an outer gatehouse. The main gatehouse with a height of 24 meters consisted of a three-storey, prismatic lower stage on a rectangular plan with the dimensions of 7.1 on 7.2 meters and a three-storey upper stage with a diameter of 4.6 and a height of 7.4 meters. At the bottom of the gatehouse there was a passage with a width of 3 meters and a height of 4 meters, enclosed with two buttresses with portcullis guides. In the south-eastern corner of the building there was a cylindrical turret probably containing an entrance and a staircase. Both stages were completed with battlements, and from the second terrace there was an eight-sided pyramid with a height of 6 meters.
Current state
To our time defense wall has survived in length of 1564 meters, but it is usually a few meters lower than the original appearance. There are also two town gates: Myśliborska from the south and Chojeńska from the west, as well as three towers and 27 half towers. The round tower called the Powder Tower is located on the north-west side, and the square tower of the Storks is the northernmost part of the fortification. The half towers are located at uneven intervals, most often from the south and south-west, less often from the east.
bibliography:
Architektura gotycka w Polsce, red. M.Arszyński, T.Mroczko, Warszawa 1995.
Kuna M., Mury miejskie Trzcińska-Zdroju, “Rocznik Chojeński”, nr 5, Chojna 2013.
Kuna M., Średniowieczne mury miejskie w powiecie gryfińskim na tle sieci miast warownych Pomorza Zachodniego i dawnej wschodniej Brandenburgii, “Rocznik Chojeński”, nr 7, Chojna 2015.